5-State Filter for very low-dynamic applications
The 5-state filter models three position states and two clock states and is only appropriate for extremely low dynamic applications (i.e., hiking). The example shown here is for a static receiver in a low multipath environment. Noise is simulated on the pseudorange measurements but the effects of the troposphere and ionosphere are assumed to have been reduced through standard correction models.
To set a baseline, an ordinary least squares (OLS) solution was performed first:
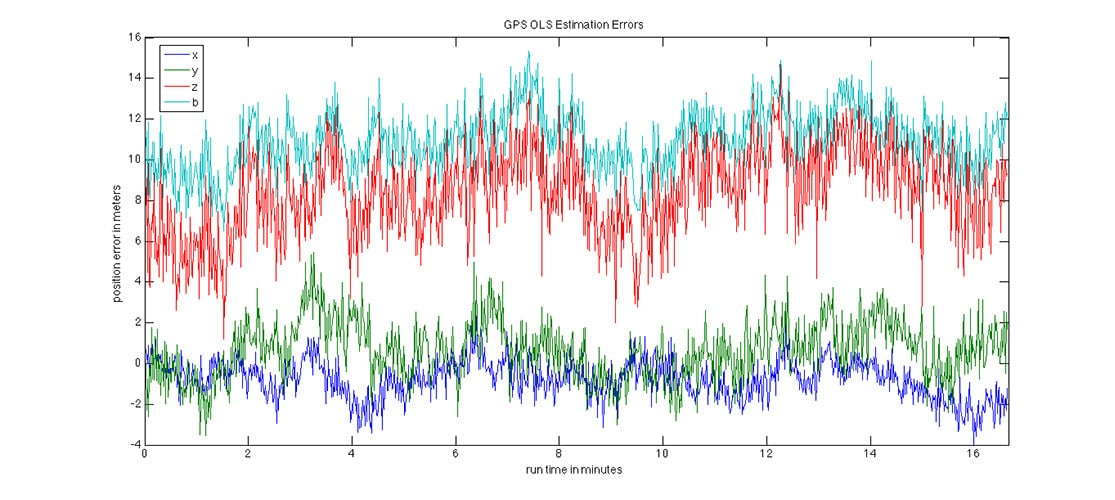
The effects of the atmospheric biases are clearly observed in the vertical position error (z) and the clock bias estimation error (b). High frequency noise and medium frequency multipath effects are observed as well.
The 5-state Kalman filter produces the following:
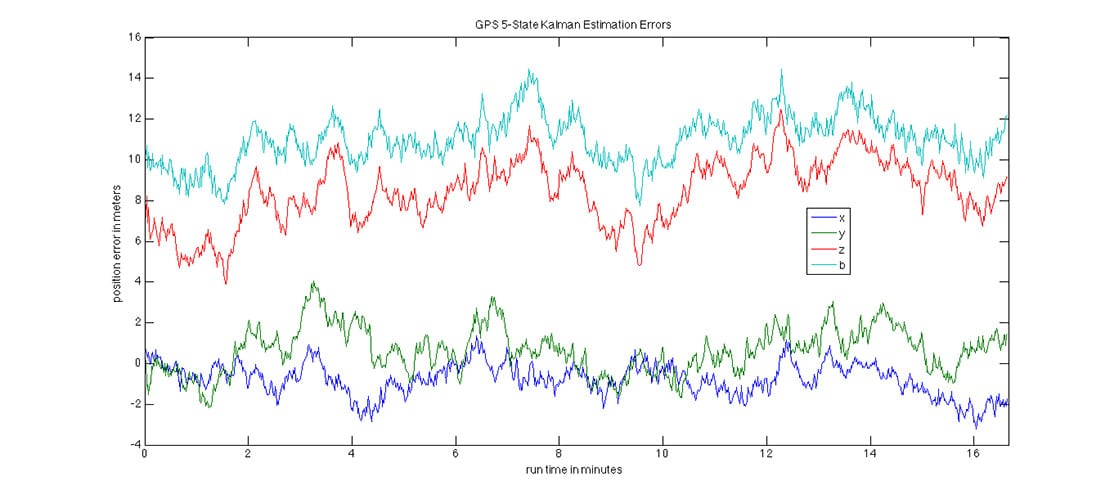
The atmospheric biases and multipath effects are still present but the filter has clearly reduced the noise significantly. Although not illustrated in this figure, this basic Kalman filter has an advantage over the OLS solution in that the filter automatically weights the measurements properly according to their contribution to the dilution of precision (DOP). In other words, the filter automatically takes the geometry into account in its estimate.
8-State Filter for Low-dynamic Applications
The 8-state filter adds three velocity states to the 5-state filter. This allows the 8-state filter to accommodate low dynamic applications. A trajectory with a 180 degree turn is used to investigate the performance of the filter:
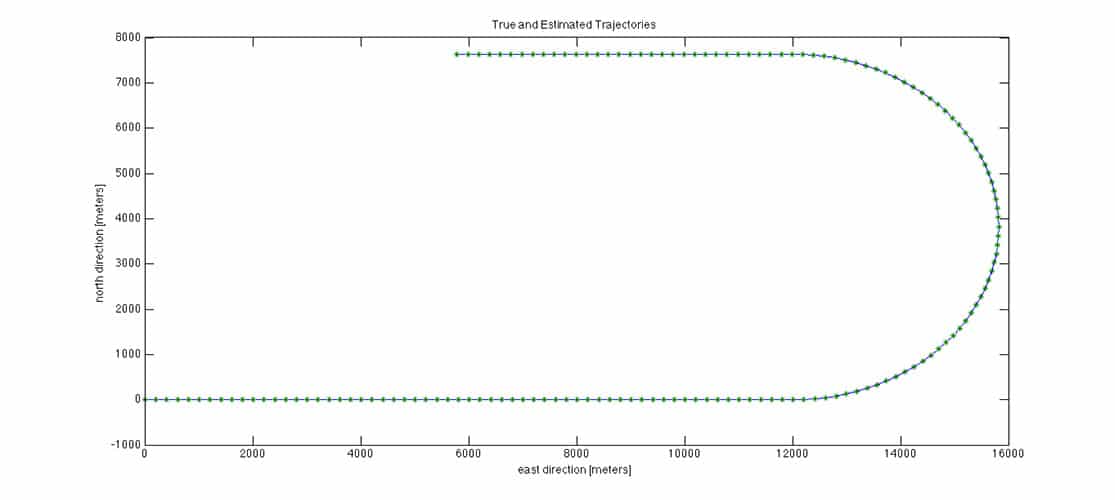
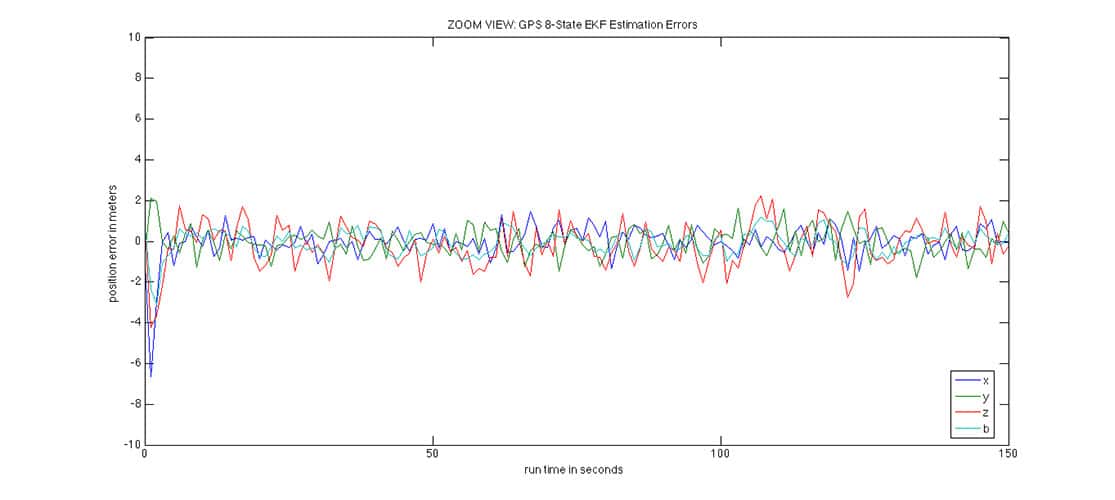
The position error is small, as expected:
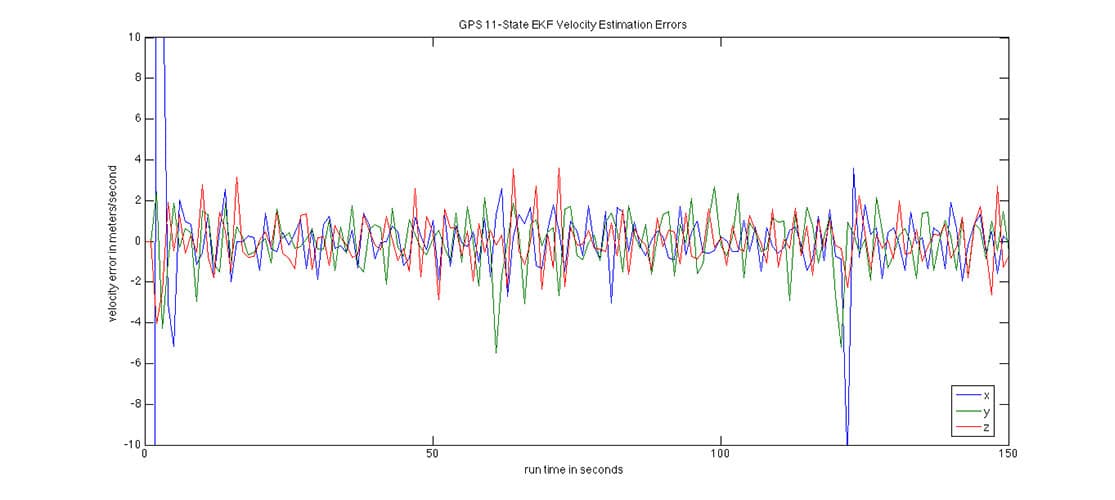
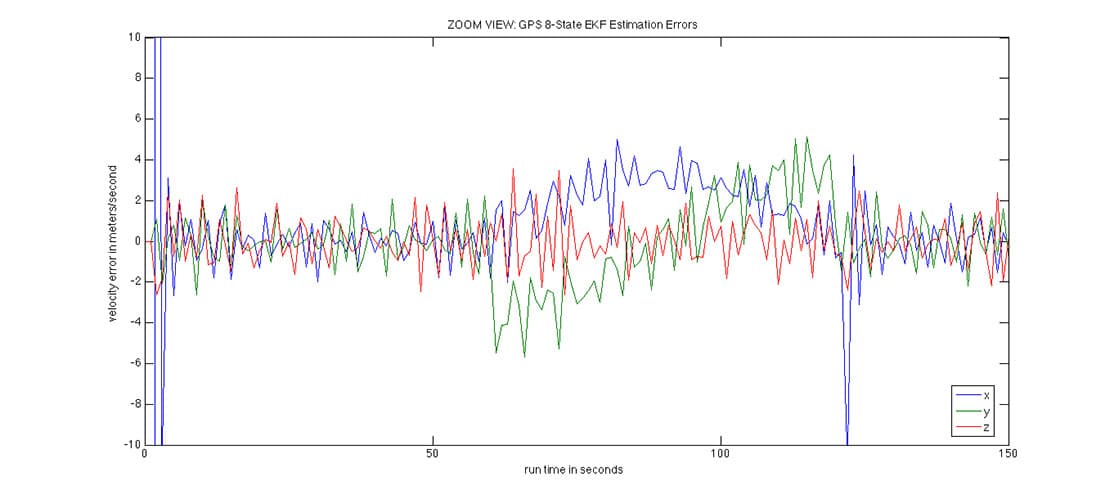
The velocity error, however, is affected by the turn since it represents medium dynamics rather than low dynamics:
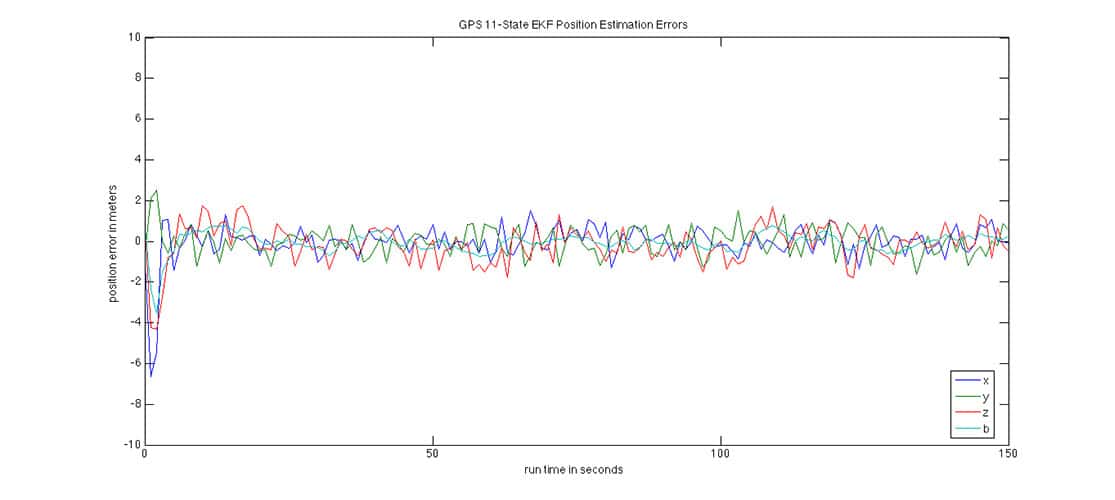
11-State Filter for medium-dynamic application
The 11-state filter adds three acceleration states to the 8-state filter and thus better accommodates the medium dynamic trajectory: